
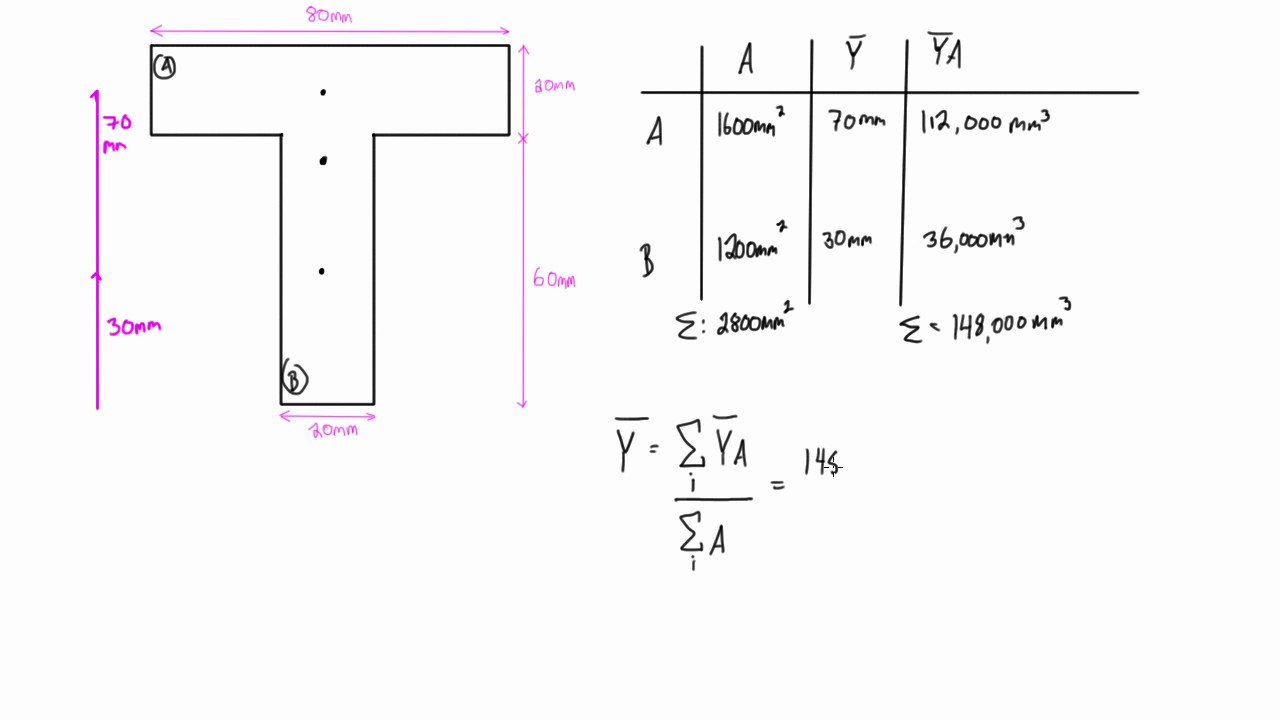
Beams - Fixed at Both Ends - Continuous and Point Loads Stress, deflections and supporting loads. Beam Loads - Support Force Calculator Calculate beam load and supporting forces. To find its distance, y_c, from a convenient axis of reference, say the lower edge of the cross-section, the first moments of area, of the web and the two flanges, relative to the same edge are employed (note: the first moment of area is defined as the area times the distance of the area centroid from the axis of reference). Area Moment of Inertia - Typical Cross Sections II Area Moment of Inertia, Moment of Inertia for an Area or Second Moment of Area for typical cross section profiles. I am hoping to use this equation along with Euler's formula to estimate the buckling force in the needle, similar to the cross section of a beam. for all the point masses that make up the object. It seems like most of the time you have to incorporate mass, but I am hoping to find area moment of inertia instead of the usually calculated mass moment of inertia. The exact location of the centroid should be therefore calculated. We defined the moment of inertia I of an object to be. However, the same cannot be said for the other axis (x-x) since no symmetry exists around it, due to the unequal flanges.

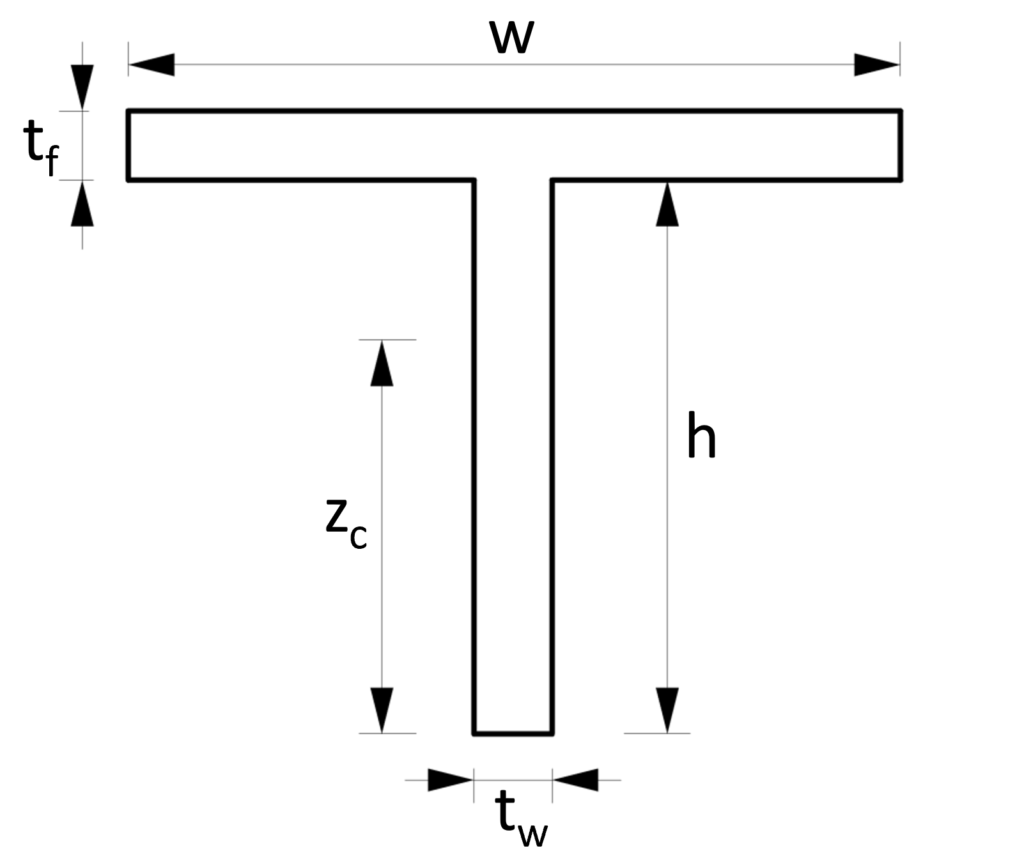
It is directly related to the area of material in the cross-section and the. The stiffness of a beam is proportional to the moment of inertia of the beam’s cross-section about a horizontal axis passing through its centroid. The second moment of area is also known as the moment of inertia of a shape. The moment of a circle area or the moment of inertia of a circle is frequently governed by applying the given equation: The. I yy b 3 H/12 + 2 (B 3 h/12) Hollow Rectangle Area Moment of Inertia Formula. I xx H 3 b/12 + 2 h 3 B/12 + hB (H+h) 2 /4 Area moment of inertia. The moments of inertia are required for the cross-section stiffness: The torsional constant IT describes the stiffness against rotation about the longitudinal. The clear height of the web, h_w that appears in above formulas, is the clear distance between the two flanges:ĭue to symmetry, around the y axis, the centroid of the cross-section must lie on the y axis too. The procedure is to divide the complex shape into its sub shapes and then use the centroidal moment of inertia formulas from Subsection 10.3.2, along with the. Second Moment of Area Formula: I Beam Area Moment of Inertia Formula. I moment of inertia (in 4) d o outside diameter (in) d i inside diameter (in) Section Modulus. Integrating curvatures over beam length, the deflection, at some point along x-axis, should also be reversely proportional to I.The area A and the perimeter P of a double-tee, with unequal flanges, can be found by the next two formulas: The area moment of inertia is a geometrical property of an area that measures how its points are distributed with regard to an arbitrary axis, providing measures of how efficiently the cross-sectional shape can resist bending caused by loading. The calculator is based on the piping formulas and equations below. However, it is crucial that b and h are assigned correct values. Solution: The moment of inertia of a rectangular shape such as this one is easily calculated by using the equation I 1/12 bh3. Determine: The Moments of Inertia, Ixx and Iyy of this section. Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I. Moment of Inertia Given: the cross-section. Making similar considerations, the moment of inertia of the angle, relative to axis y0 is:


 0 kommentar(er)
0 kommentar(er)
